Версия для печати темы
Нажмите сюда для просмотра этой темы в обычном формате
Образовательный студенческий форум _ Линейная алгебра и аналитическая геометрия _ Правильно ли составил систему
Автор: Spartak 23.11.2007, 19:49
Я начал решать одно задание:
Даны вектора а1 (5, 1, -7, 2), а2 (2, -3, -1, -9), а3 (-7, -1, 1, -2), а4 (3, 4, -5, -6). Показать, что эти вектора образуют базис четырёхмерного пространства, найти координаты вектора в (59, 20, -38, -53) в этом базисе.
Составил матрицу, нашел определитель ( равен 3150), доказал что образуется базис.
Для дальнейшего решения нужно составить систему ( посоветовал venja).
Составил. Вы не могли бы мне сказать - правильно я её составил или нет.
Система на фото.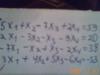
Автор: venja 24.11.2007, 4:53
Я начал решать одно задание:
Даны вектора а1 (5, 1, -7, 2), а2 (2, -3, -1, -9), а3 (-7, -1, 1, -2), а4 (3, 4, -5, -6). Показать, что эти вектора образуют базис четырёхмерного пространства, найти координаты вектора в (59, 20, -38, -53) в этом базисе.
Составил матрицу, нашел определитель ( равен 3150), доказал что образуется базис.
Для дальнейшего решения нужно составить систему ( посоветовал venja).
Составил. Вы не могли бы мне сказать - правильно я её составил или нет.
Система на фото.
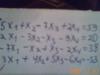
Не так.
Пусть х1, х2, х3, х4 - искомые координаты. Тогда должно выполняться
х1*а1+х2*а2+х3*а3+х4*а4=в
Расписывая это векторное равенство ПОКООРДИНАТНО, получим систему для определения х1, х2, х3, х4 :
5х1+2х2-7х3+3х4=59
...............................
...............................
...............................
Автор: Spartak 24.11.2007, 10:15
Слушай, а у меня по моему также.
5х1+2х2-7х3+3х4=59
2х1-3х2-х3-9х4=20
и так далее роде у меня тоже так на фото
Автор: venja 24.11.2007, 10:50
Да не так.
Должно быть
5х1+2х2-7х3+3х4=59
х1-3х2-х3+4х4=20
-7х1-х2+х3-5х4=-38
2х1-9х2-2х3-6х4=-53
Автор: Spartak 24.11.2007, 16:25
Спасибо. Шас попробую разобраться во всём.
Автор: Руководитель проекта 24.11.2007, 18:32
Слушай, а у меня по моему также.
А в вашем вузе к преподавателям принято обращаться на «ты»?
Автор: Spartak 24.11.2007, 20:59
Руководитель проекта,
Извиняюсь, в следубщий раз бращусь на Вы. В нашем вузе преподаватели нас за людей не считают, без вопросов, не знаешь - неуд.
Автор: Руководитель проекта 24.11.2007, 21:26
Не могу с вами согласиться. Думаю, что это лишь только ваше мнение.
Автор: Spartak 25.11.2007, 10:03
Ну я заочник, может в этом дело.
Автор: Spartak 25.11.2007, 18:46
Люди, извините что беспокою. Я вам наверное уже надоел.
Вопрос насчёи системы. Начал я её решать методом Крамера. Но это очень долгий путь, занимает много времени. Да ешё и ответы какие-то плохие получаются, точнее неправельные. На экзамене не успеешь решить. Методом Гауса не понимаю как решать. Вроде с элементарными преобразованиями разобрался на простых примерах, а на этом не могу ( большие и сложные числа). Может есть какой-то другой реальный способ, более быстрый, а то на экзамене не успею решить????????????
Автор: Julia 27.11.2007, 7:11
Есть еще метод - матричный. Если у вас нет проблем с нахождением обратной матрицы, то это - для вас.
Хотя метод Гаусса более универсальный, подходит для системы с любым количеством уравнений и неизвестных.
Автор: Spartak 27.11.2007, 7:18
Решил эту систему.
х1=0, х2=3, х3=-5, х4=6.
Гдето методом Крамера, где-то подбором но всётаки решил. Хотя о методе Гауса хотелось бы узнать поподробнее, чтоб на экзамене было увереннее. Всем огромное спасибо. Уже почти доделал свою контрольную.
Русская версия Invision Power Board (http://www.invisionboard.com)
© Invision Power Services (http://www.invisionpower.com)
