Версия для печати темы
Нажмите сюда для просмотра этой темы в обычном формате
Образовательный студенческий форум _ Дифференцирование (производные) _ dz/dx - ?
Автор: Mr.BRAUN 7.6.2013, 3:59
Всем привет, не знаю туда пишу или нет.
Помогите найти dz/dx и dz/dy
z=cos(ln(xy))
dz/dx= -sin(ln(xy))*1/xy
dz/dy= -sin(ln(xy))*1/xy
Так или нет?
Автор: Julia 7.6.2013, 4:24
Не совсем.
dz/dx= -sin(ln(xy))*1/xy*(xy)'=-sin(ln(xy))*1/x
dz/dy= -sin(ln(xy))*1/xy*(xy)'=-sin(ln(xy))*1/y
Автор: Mr.BRAUN 7.6.2013, 4:30
Не совсем.
dz/dx= -sin(ln(xy))*1/xy*(xy)'=-sin(ln(xy))*1/x
dz/dy= -sin(ln(xy))*1/xy*(xy)'=-sin(ln(xy))*1/y
у меня вопрос
dz/dy= -sin(ln(xy))*1/xy*(xy)'=-sin(ln(xy))*1/y
почему еще надо умножать на (xy)' ?
Автор: Kisuni 7.6.2013, 5:03
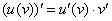
Вот здесь подробно разбирают: http://mathprofi.ru/proizvodnaya_slozhnoi_funkcii.html
Автор: Julia 10.6.2013, 1:55
у меня вопрос
dz/dy= -sin(ln(xy))*1/xy*(xy)'=-sin(ln(xy))*1/y
почему еще надо умножать на (xy)' ?
Потому что ln(xy) - сложная функция с аргументом xy.
Русская версия Invision Power Board (http://www.invisionboard.com)
© Invision Power Services (http://www.invisionpower.com)
