Версия для печати темы
Нажмите сюда для просмотра этой темы в обычном формате
Образовательный студенческий форум _ Интегралы _ Решить неопределенные интегралы
Автор: Bobik 2.6.2012, 9:04
Помогите,пожалуйста, дорешать интегралы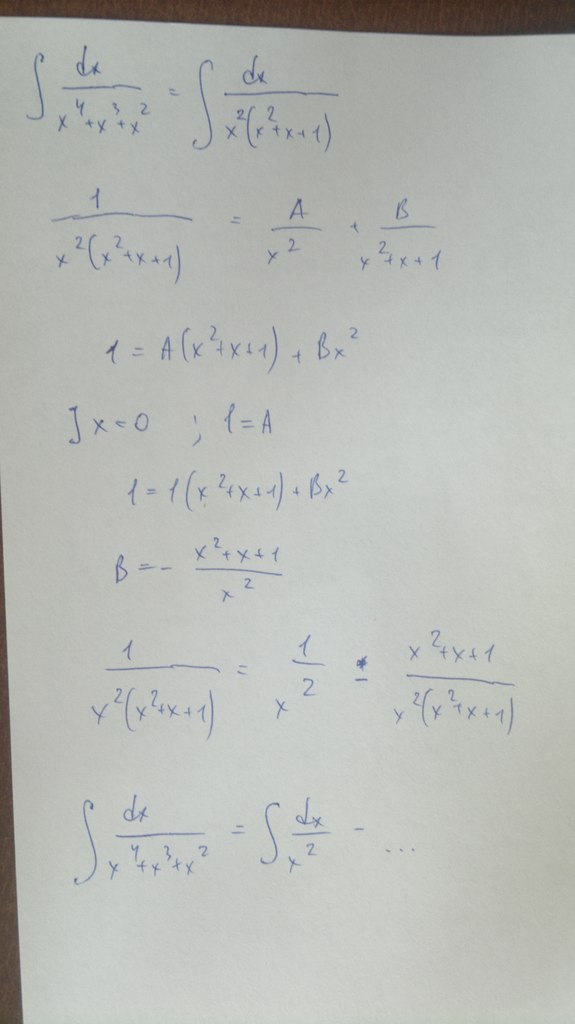
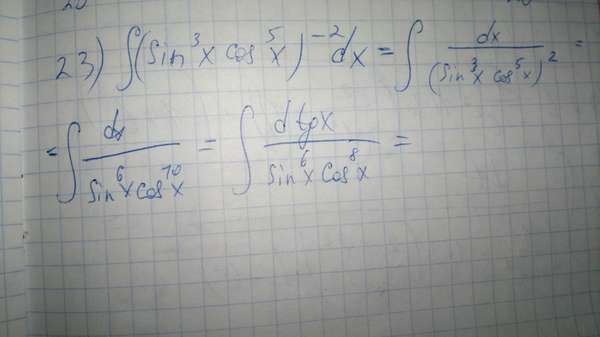

Автор: tig81 2.6.2012, 9:09
1. Неправильно раскладываете на простейшие дроби (вторая строка), вторая дробь: в числителе должен быть многочлен степени на 1 меньше, чем знаменателе, у вас в знаменателе степень 2, а в числителе 0
+ нет еще дроби вида С/х, которая относится к кратному корню 0
23. Попробуйте замену tgx=t
17. Я бы посоветовала не раскладывать на два интеграла, а сразу имеющуюся дробь раскладывать на простейшие
Автор: Bobik 2.6.2012, 9:15
1. Неправильно раскладываете на простейшие дроби (вторая строка), вторая дробь: в числителе должен быть многочлен степени на 1 меньше, чем знаменателе, у вас в знаменателе степень 2, а в числителе 0
+ нет еще дроби вида С/х, которая относится к кратному корню 0
23. Попробуйте замену tgx=t
17. Я бы посоветовала не раскладывать на два интеграла, а сразу имеющуюся дробь раскладывать на простейшие
Спасибо!Буду пробовать!
Автор: tig81 2.6.2012, 9:18
![]() Удачи!
Удачи!
Автор: Bobik 2.6.2012, 10:27
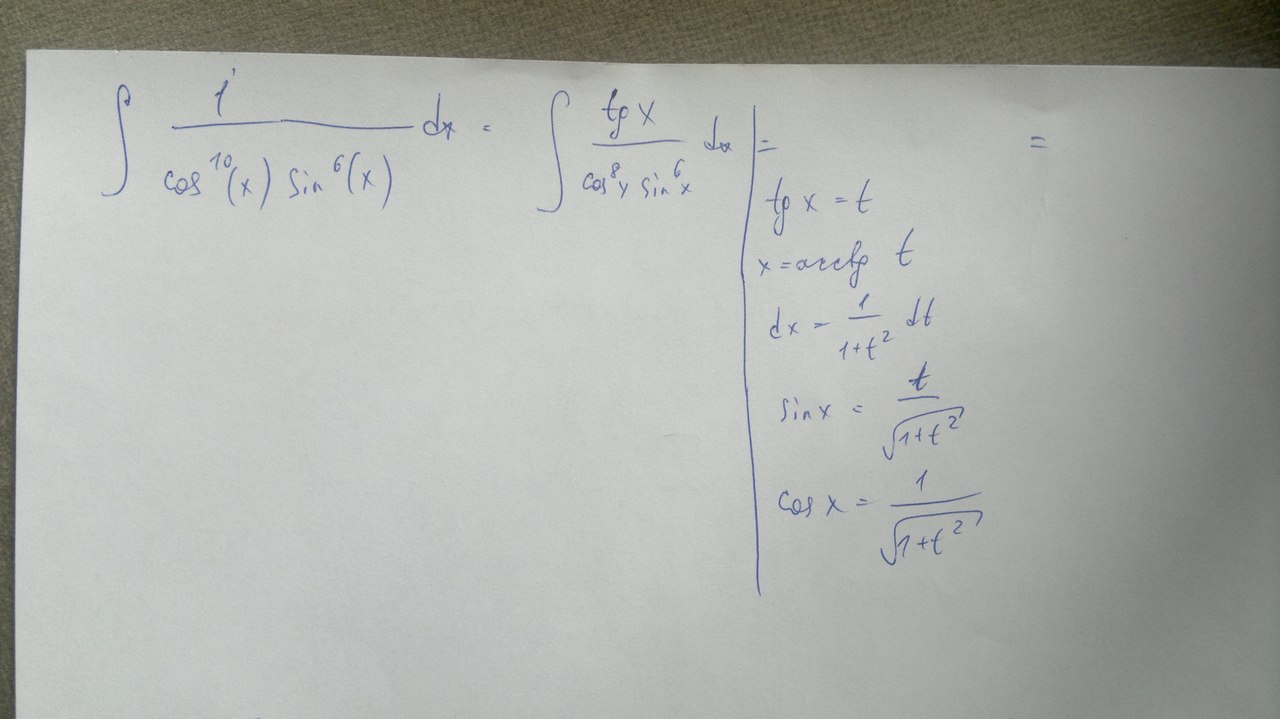
при подстановке какой-то бред получается
а другие решил разложением на простейшие,как вы посоветовали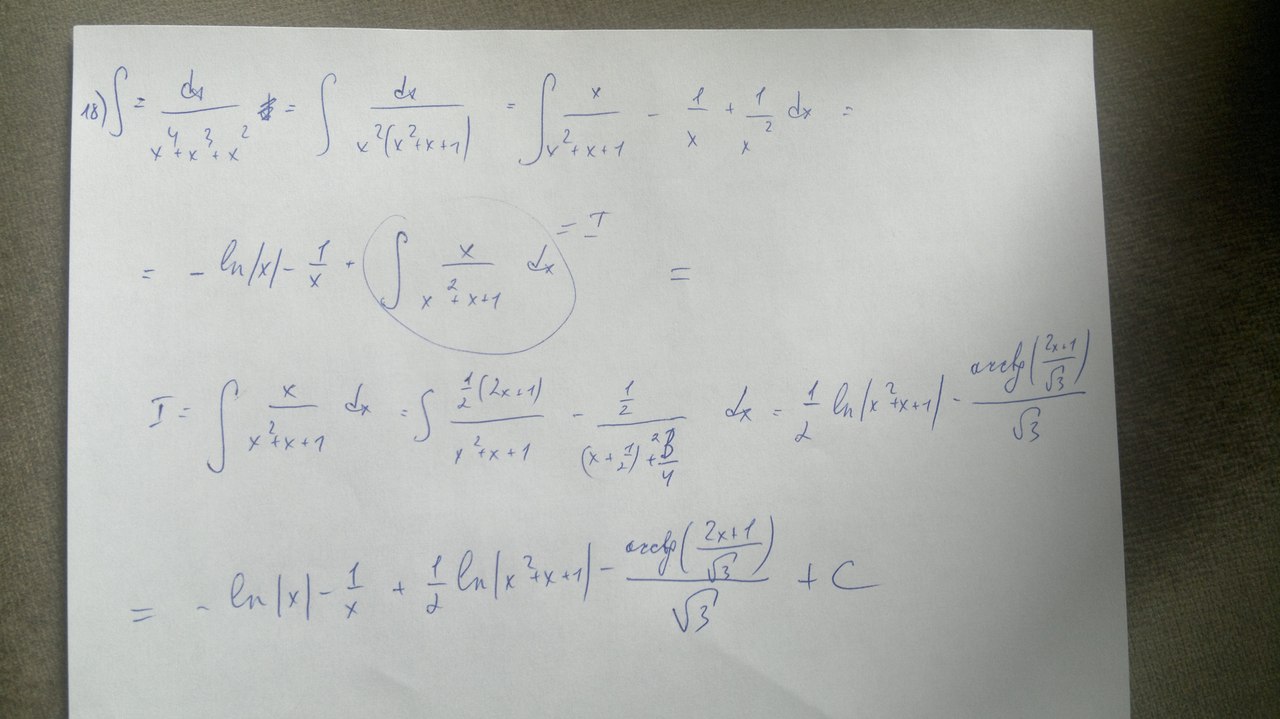
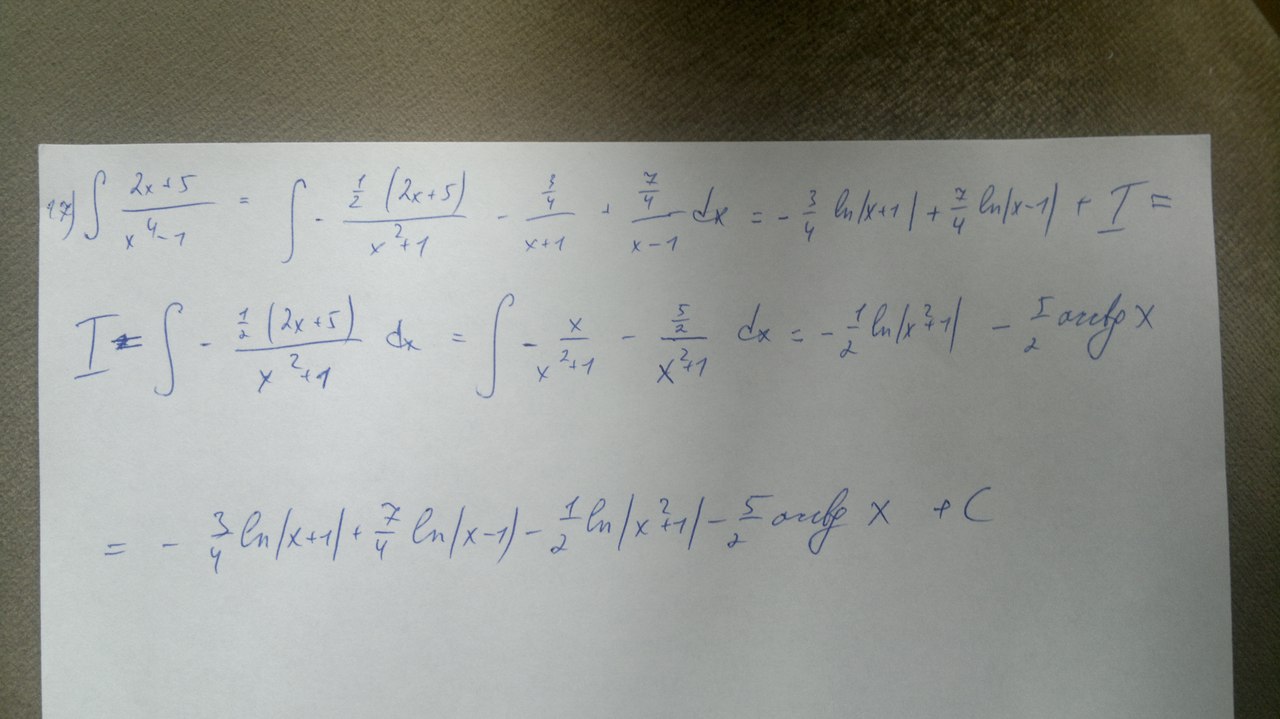
Автор: Dimka 2.6.2012, 10:38
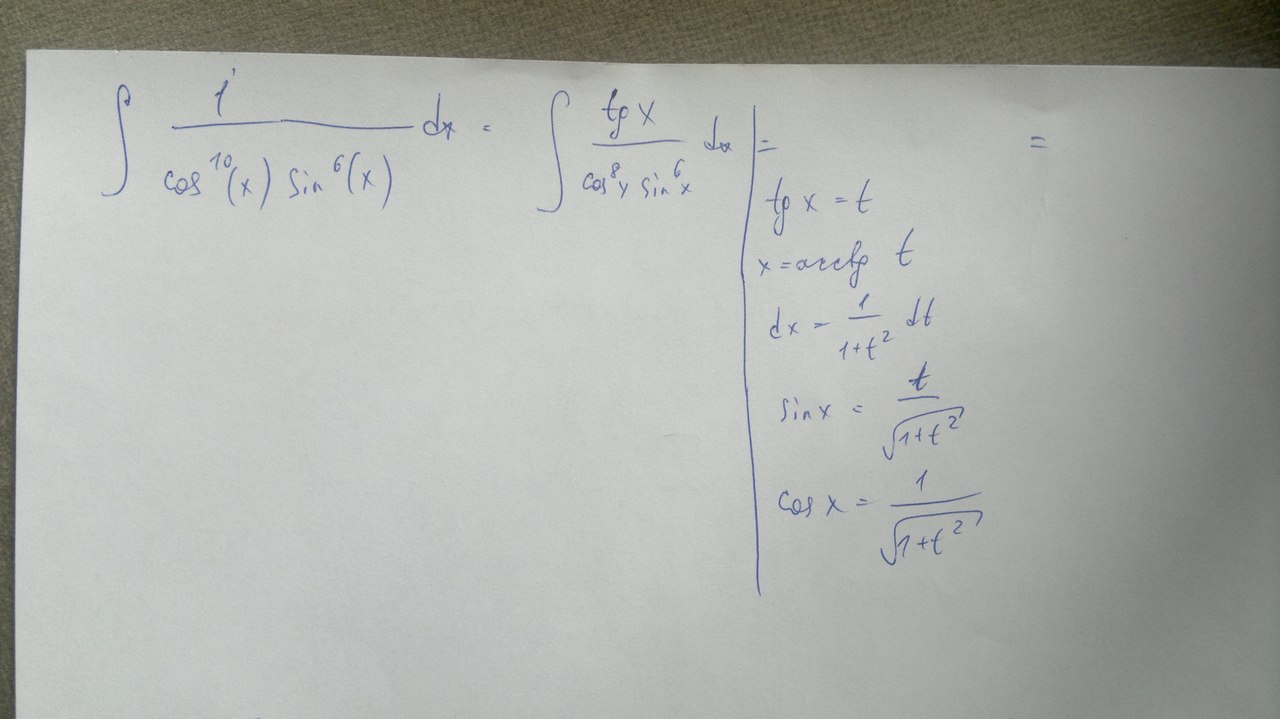
при подстановке какой-то бред получается
откуда tgx в числителе взялся?
Автор: Bobik 2.6.2012, 10:44
откуда tgx в числителе взялся?
1/cos^2 x - производная тангенса, в числите должно быть dtgX, если не ошибаюсь
Автор: Dimka 2.6.2012, 11:28
У Вас какая то каша.
Откройте любой учебник и посмотрите тему интегрирование тригонометрических функций. (Универсальная тригонометрическая подстановка)
Автор: tig81 2.6.2012, 11:29
Откройте любой учебник и посмотрите тему интегрирование тригонометрических функций. (Универсальная тригонометрическая подстановка)
а что, универсалкой будет проще?
Автор: Dimka 2.6.2012, 11:36
не обязательно. Можно под дифференциал tgx загнать, а под интегралом все преобразовать к tgx. В конце простое выражение получится
Автор: tig81 2.6.2012, 11:41
не обязательно. Можно под дифференциал tgx загнать, а под интегралом все преобразовать к tgx. В конце простое выражение получиться
так я ж выше такое и предлагала
Автор: Bobik 2.6.2012, 11:46
не обязательно. Можно под дифференциал tgx загнать, а под интегралом все преобразовать к tgx. В конце простое выражение получиться
хорошая идея!
Автор: Bobik 2.6.2012, 17:06
не обязательно. Можно под дифференциал tgx загнать, а под интегралом все преобразовать к tgx. В конце простое выражение получится
никак не получается решить пример!=(
Еще можно попробовать решить его с помощью сёкансов и косёкансов, но наш преподаватель это не одобрит!
Автор: tig81 2.6.2012, 17:52
показывайте как решали
Автор: Bobik 2.6.2012, 18:57
показывайте как решали
Вроде осилили,товарищ помогал, правда,не самым компактным образом!=)

Автор: tig81 2.6.2012, 19:10
а как интеграл преобразовали в сумму двух (первая строка)?
Автор: Bobik 2.6.2012, 19:17
а как интеграл преобразовали в сумму двух (первая строка)?
Воспользовались тригонометрическим тождеством sin^2 x + cos^2 x = 1
Автор: Bobik 2.6.2012, 19:56
может предложите решение по короче, например с дифференцированием тангенса, интересно было бы посмотреть!
Автор: tig81 2.6.2012, 21:00
может предложите решение по короче, например с дифференцированием тангенса, интересно было бы посмотреть
Вам же написали замену, в чем возникли проблемы?
Автор: Bobik 3.6.2012, 8:17
Вам же написали замену, в чем возникли проблемы?
с подстановкой и упрощением
Автор: Dimka 3.6.2012, 8:25
Вам же написали замену, в чем возникли проблемы?
Дальше упрощайте (возводите в степени)

Автор: Bobik 3.6.2012, 9:14
Дальше упрощайте (возводите в степени)

вот как раз после этого действия и дальнейшего упрощения у меня пошли косяки,а в числители получалась куча Т-шек с большими степенями,а в знаменателе Т в шестой степени...точно как было не скажу,черновики были беспощадно уничтожены,ибо пол дня штудировать один интеграл, несколько, замучило!)В принципе, уже решение интеграла есть...поэтому , можете не тратить на него свое время, а я так спрашиваю чисто для общего развития!=)
Автор: Dimka 3.6.2012, 9:19
В принципе, уже решение интеграла есть...поэтому , можете не тратить на него свое время, а я так спрашиваю чисто для общего развития!=)
тогда тема закрывается
Русская версия Invision Power Board (http://www.invisionboard.com)
© Invision Power Services (http://www.invisionpower.com)
