Версия для печати темы
Нажмите сюда для просмотра этой темы в обычном формате
Образовательный студенческий форум _ Теория вероятностей _ условная энтропия квантового сигнала
Автор: samik 26.2.2012, 6:13
добрый день!
необходимо найти условную вероятность квантового сигнала с распределением Р с точностью 1В. условные вероятности уровней заданны матрицей Р(х/у). уровни 0В, 1В, 2В.
подскажите пожайлуста, с чего начать? не знаю даже с какой стороны подойти!
матрица представлена на картинке!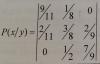
Автор: malkolm 26.2.2012, 14:11
Например, рассказать нам, что такое "условная вероятность квантового сигнала с точностью 1В" :\
Автор: samik 27.2.2012, 11:30
условная вероятность это вероятность одного события при условии, что другое событие уже произошло.
квантовый сигнал это сигнал разбитый на уровни, количество которых должно быть представлено в числах заданной разрядности. Расстояния между этими уровнями называется шагом квантования Δ. Число этих уровней равно N (от 0 до N-1). Каждому уровню присваивается некоторое число. Отсчёты сигнала сравниваются с уровнями квантования и в качестве сигнала выбирается число, соответствующее некоторому уровню квантования. Каждый уровень квантования кодируется двоичным числом с n разрядами. Число уровней квантования N и число разрядов n двоичных чисел, кодирующих эти уровни, связаны соотношением n ≥ log2(N).
связать два этих понятия у меня не получается, хотя есть предположения! преподаватель, который дал задание находится в командировке, поэтому я обратился к Вам за помощью!
Автор: malkolm 27.2.2012, 12:21
Вот видите - "одного события при условии, что другое событие". Как понять, что такое "условная вероятность квантового сигнала" - где тут указанные два события?
Условные вероятности уровней - это опять-таки условные вероятности одного события при условии другого. Что за события, из объяснений не стало понятно. Боюсь, Вам придётся-таки ждать преподавателя. Условие задачи отсутствует, квантование тут ни при чём совершенно.
Автор: samik 27.2.2012, 12:49
я ранее допустил ошибку!
нужно:
найти полную условную энтропию квантового сигнала с распределением Р с точностью.....
извиняюсь за свою невнимательность!
Автор: malkolm 28.2.2012, 11:53
Ну так и в чём сложность тогда? Ищем определение условной энтропии, подставляем готовые вероятности, вот и всё.
Автор: samik 28.2.2012, 15:37
попробовал решить используя формулу условной энтропии!
проверте пожайлуста! решение здесь:
http://imglink.ru/pictures/28-02-12/a927d90beddf30a411b497e40d0cfad3.jpg
не уверен что правильно понял для чего уровни 0В, 1В, 2В и как быть с точностью 1В?
Автор: malkolm 28.2.2012, 16:29
Точность 1В задана тем, что значения у Вас 0В, 1В, 2В.
О Вашем решении: в формуле p(yi / xi), а Вы вместо них подставляете p(xi / yj) из таблицы. Внизу вероятности p(xi) равные 0, 1, 2 - это Вы всерьёз?
На всякий случай: в данной таблице приведено три столбика. Первый столбец - это условное распределение икса при y=0 (0В). Т.е. P(X=0 | Y=0)=9/11, P(X=1|Y=0)=2/11. Второй столбец - условное распределение икса при Y=1 (1В). Третий - при Y=2.
Условное (и безусловное тоже) распределение игрека в условии задачи не задано никак вообще. И ниоткуда вычислено быть не может. Поэтому об отыскании условной энтропии игрека по иксу не может идти и речи. Если только в таблице не перепутано обозначение, и это не P(y/x).
Там что-то говорится о распределении P - где оно вообще? Не условные вероятности, а само распределение?
Автор: samik 29.2.2012, 13:41
я думаю что в задании ошибка и правильно будет p(yi / xi). распределение обозначено как просто Р и все.
не обязательно же искать энтропию игрека по иксу, можно же найти энтропию икса от игрека или я что то путаю?
чему равны p(xi) я не понимаю. есть предположение что они равны просто распределению Р.
попробовал переделать. получилось так:
http://imglink.ru/pictures/29-02-12/e82feefa0e8f5c91de2156f268000915.jpg
если Вам не трудно проверьте еще две задачи!
вот первая:
http://imglink.ru/pictures/29-02-12/749962fd55994a34f11dc7bab0043cad.jpg
вот задание второй:
http://imglink.ru/pictures/29-02-12/68276574b9ff491b752d0252ab575169.jpg
а тут решение:
http://imglink.ru/pictures/29-02-12/175c1655d799924f3dfb38668261f505.jpg
Автор: malkolm 29.2.2012, 14:37
Ну так - другое дело. Да, они равны просто распределению P, которое в условии не дано. Но оно какое-то есть.
В задаче про дни рождения второй вопрос мне непонятен, но, наверное, Вы знаете, что делаете ![]()
Последняя задача - такая же, как Вы уже решили, только исходное распределение дано. Всё верно.
Автор: samik 29.2.2012, 15:38
спасибо Вам за помощь!
Автор: malkolm 29.2.2012, 19:32
Да не за что, Вы и сами неплохо справляетесь.
Русская версия Invision Power Board (http://www.invisionboard.com)
© Invision Power Services (http://www.invisionpower.com)