Версия для печати темы

Автор: Lutik 22.2.2012, 14:48

Здравствуйте!
Помогите пожалуйста с исследованием функции по производной.
y=(x-2)^2*e^(-x)
R (-00;+00)
Производная у'=-e^(-x)(x^2-6x+8)
Приравниваем к нулю -e^(-x)*(x^2-6x+8)=0
-e^(-x)=0
x^2-6x+8=0; х1=2; х2=4
(х-2)(х-4)=0
Следовательно, на промежутках (-00;2] U [4;+00) производная положительна, функция возрастает.
на интервале (2;4) отрицательна, функция убывает.
Точка х1=2 является точкой максимума, так как справа от этой точки функция убывает, а слева - возрастает. В этой точке значение функции равно у(2)=0.
Точкой минимума является точка х2=4. В этой точке значение функции равно у(4)=4*е^(-4).

Не пойму что с функцией -e^(-x)=0, при (-00;+00) ?
Правильно исследую?

Автор: A_nn 22.2.2012, 16:17

В принципе - правильно, цифры проверять не в состоянии. Ищите асимптоты (наклонные, правую и левую - отдельно).

А, или Вы про равенство экспоненты 0?? Постройте график экспоненты, и посмотрите, где он пересекает ось Ох.

Автор: Lutik 22.2.2012, 16:59

Построил у=-e^(-x)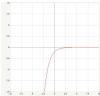

Наклонная асимптота: lim (+-00) ((x-2)^2*e^(-x))/x)
Вертикальных асимптот нет, так как (x-2)^2/e^(x), то e^(x) не равно нулю
Правильно?

Автор: A_nn 22.2.2012, 18:05

....кто, интересно...

Предел надо найти (две штуки).
Вертикальных нет, это правда (хотя Ваши логические выводы выглядят странно).

Автор: Lutik 22.2.2012, 18:21

Вертикальных асимптот нет, так как функция принадлежит всей числовой оси (-00; +00).
Горизонтальная асимптота lim x->(+-00) (x-2)^2*e^(-x)=0
Наклонная асимптота kx+b: lim x->(+-00) ((x-2)^2*e^(-x))/x=0. Это мы нашли k.
b находится lim x->(+-00) ((x-2)^2*e^(-x) - kx), то есть lim x(-00; +00) ((x-2)^2*e^(-x))=0, наклонной асимптоты нет.

Автор: A_nn 22.2.2012, 18:26

Непонятно, к чему стремится х - где к +беск, где к -.
Это большая разница

И функция оси принадлежать не может. Она никому не принадлежит, она свободна. Вот ее ОДЗ - да, принадлежит. Но это еще не говорит об отсутствии вертикальных асимптот.

Т.е. нет, даже ОДЗ не принаджлежит, конечно Его точки только.

Автор: Lutik 22.2.2012, 18:37

да я просто не правильно сформулировал
не так написал.
x -> +-00

Автор: A_nn 22.2.2012, 18:52

Но там разные пределы, когда + и когда -.

Автор: Lutik 22.2.2012, 19:00

да, но в моём случае получается ноль и значит наклонной асимптоты нет

Автор: A_nn 22.2.2012, 19:04

горизонтальная есть - это частный случай наклонной.
А когда 0-то получается? В + или в -? Вот в чем вопрос...

Автор: Lutik 22.2.2012, 19:11

при +00 будет 0, при -00 будет 00

Автор: A_nn 22.2.2012, 19:13

Угу. И какой вывод? Какая ас-та?

А как Вы, интересно, догадались, что этот предел =0?

Автор: Lutik 22.2.2012, 19:31

Асимптота есть только горизонтальная Х=0

Автор: A_nn 22.2.2012, 19:41

левая или правая?


А точки перегиба искать нужно?

Автор: Lutik 22.2.2012, 19:47

правая асимптота
точки перегиба по второй производной
y''=((x-2)^2*e^(-x))''= e^(-x)(x^2-8x+14)
приравниваем к нулю: e^(-x)=0 и x^2-8x+14=0
e^(-x)=0 на (-00; +00)
x^2-8x+14=0
х=4+корень2
х=4-корень2
на числовой оси +-+
вторая производная положительная, то выпуклость вниз

Автор: A_nn 22.2.2012, 19:58

Числа не проверяю, ок?
Стройте, там все ясно станет.

Автор: Lutik 22.2.2012, 20:14

Спасибо! Цифры правильные, я проверял несколько раз.

Автор: Lutik 23.2.2012, 10:19

Про минимум и максимум: по графику минимум в точке х=2, максимум в х=4.

При исследовании выражения:
x^2-6x+8=0; х1=2; х2=4
(х-2)(х-4)=0
На числовой оси +-+
Следовательно, на промежутках (-00;2] U [4;+00) производная положительна, функция возрастает.
на интервале (2;4) отрицательна, функция убывает.
Точка х1=2 является точкой максимума, так как справа от этой точки функция убывает, а слева - возрастает. В этой точке значение функции равно у(2)=0.
Точкой минимума является точка х2=4. В этой точке значение функции равно у(4)=4*е^(-4).

По графику видно что минимум в х=2, но в выражении х=4, не пойму в чём ошибка.




Эскизы прикрепленных изображений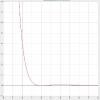

Автор: A_nn 23.2.2012, 10:24

Проверьте знаки производной

Автор: Lutik 23.2.2012, 10:31

Корни 2 и 4, (х-2)(х-4)=0, знаки будут слева-направо +-+, при 0 будет -*- = +, при 3 будет +*-=-, при 5 будет +*+=+

Автор: A_nn 23.2.2012, 10:34

Да нет, Производной, а не этого выражения. В НЕПРЕОБРАЗОВАННОМ виде!

Автор: Lutik 23.2.2012, 10:47

Также получается и в x^2-6x+8=0, при 0 будет 8, при 3 будет -1, при 5 будет 3 (+-+). Или надо ещё учитывать -e^(-x)(x^2-6x+8)?
Да тогда всё верно надо подставлять в -e^(-x)(x^2-6x+8), тогда будет -+-, всё сходится.
Спасибо!!!

Автор: A_nn 23.2.2012, 10:49

Ну конечно....

Автор: Lutik 26.2.2012, 10:58

Спасибо большое за помощь!