Версия для печати темы

Автор: behappy 8.2.2012, 11:12

1. Радиусы оснований усеченного конуса 3 и 6 дм, а образующая 5 дм.
Найдите: а) высоту усеченного конуса; б) площадь его осевого сечения; в) угол наклона образующей к плоскости основания

2. Радиусы оснований усеченного конуса R и r, площадь осевого сечения S. В усеченный конус вписана усеченная пирамида, основанием которой служит прямоугольный треугольник с острым углом Альфа.Найдите площадь боковой поверхности усеченной пирамиды.

3. Радиусы оснований усеченного конуса относятся как 1:3, образующая составляет с плоскостью основания угол 45 градусов, высота равна h. Найдите площади оснований

4. Радиусы оснований усеченного конуса равны R и r. Высота разделена на три равные части, и через точки деления проведены плоскости, параллельные основанию. Найдите площади сечений.

Автор: граф Монте-Кристо 8.2.2012, 16:24

Ваши идеи?

Автор: venja 8.2.2012, 16:59

Мои.

Автор: Diligent 9.2.2012, 0:49

Задача № 1.

Указание к решению задачи.

1) Зная длины отрезков AO_1 и HO_1, найдите длину отрезка AH (см. рис.).

2) В прямоугольном треугольнике ABH известны катет AH и гипотенуза AB. Следовательно, по теореме Пифагора можно найти другой катет BH.
(это длина высоты усечённого конуса).

3) Площадь трапеции ABCD (осевого сечения) можно найти по двум основаниям AD, BC и высоте BH.

4) Угол наклона образующей к плоскости основания (это угол BAH) можно найти из прямоугольного треугольника ABH, используя тригонометрические функции.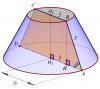

Автор: Diligent 9.2.2012, 2:35

Рисунок к задаче № 2.

Автор: Руководитель проекта 11.2.2012, 7:36

Diligent, подскажите, пожалуйста, название программы, в которой можно делать такие красивые рисунки.

Автор: Diligent 11.2.2012, 14:40

Здравствуйте! Такие рисунки можно сделать с помощью программы "Живая Геометрия".

Автор: tig81 11.2.2012, 15:26

Спасибо.
Вот скачала отсюда http://math66.ucoz.ru/load/2-1-0-6
А здесь вроде как он-лайн http://www.geogebra.org/webstart/geogebra.html
Это о, о чем вы говорили?

Автор: Diligent 11.2.2012, 17:36

Нет, это не та программа. Речь шла о программе "Portable Geometer's Sketchpad".

Хотя говорят, что в программе "GeoGebra" больше возможностей, чем в "Portable Geometer's Sketchpad".

Автор: tig81 11.2.2012, 17:44

Ясно, спасибо, посмотрим.

Автор: Руководитель проекта 11.2.2012, 20:14

Diligent, tig81. Спасибо за информацию.

Автор: tig81 11.2.2012, 20:31

Автор: Diligent 11.2.2012, 22:32

Пожалуйста!

Автор: ОляКроля 9.5.2012, 16:56

В треугольнике АВС АС=ВС, АВ = 18. cos A = 0,6 Найдите АС.

Помогите пожалуйста!

Автор: venja 9.5.2012, 17:10

Опустите высоту (она же будет и медианой) СD и рассмотрите треугольник ACD.

Автор: Dimka 9.5.2012, 19:24

Весна, однако. Пора, батенька, девок рассматривать, а не треугольники