Версия для печати темы

Автор: samik 28.1.2012, 10:32

Добрый день!
Прошу помощи в решении задачи. Вот условие:

Производившиеся в некотором районе многолетние наблюдения показали ,что из 100 000 детей , достигшие десятилетнего возраста , до 40 лет доживает в среднем 82 277 , а до 70 лет -37 977. Найти вероятность того ,что если человек достигнет сорокалетнего возраста, то он доживет и до 70 лет?

Начал решать:
нашел вероятность дожить до 40 и вероятность дожить до 70

Р(А)=82277/100000 и Р(В)=37977/100000

что делать дальше не знаю. так как события зависимы, то наверное нужно либо сложить либо перемножить вероятности. помогите разобраться.

заранее спасибо!

Автор: malkolm 28.1.2012, 12:46

См. определение условной вероятности.

Автор: samik 28.1.2012, 14:58

посмотрел определение, из него следует:

Ра(В)=Р(АВ)/P(A);
P(A)-эту вероятность я нашел;
Р(АВ)-произведение зависимых событий, нашел по формуле:

Р(АВ)=Р(А)*Р(В/А)=0,82277*(0,37977/0,82277)=0,37977- не знаю на сколько правильно я воспользовался данной формулой.

в итоге получил

Ра(В)=0,37977/0,82277=0,4616-вероятность дожить до70 лет увеличила вроде правильно, но меня смущает данная формула и ее результат:

Р(АВ)=Р(А)*Р(В/А)!

очень жду Ваших коментариев!

заранее благодарен!

Автор: malkolm 28.1.2012, 18:11

Ищем P(B|A), для этого вычисляем P(B|A) = P(AB)/P(B ), а P(AB ) = P(A)*P(B|A), после чего подставляем известное P(B|A), сокращаем, получаем P(B|A). Ничего не смущает в этой абсурдной последовательности? Чем отличается P(B|A) от Pa(B )?

Ответ P(B|A) = 0,37977/0,82277=0,4616.

Автор: samik 29.1.2012, 4:27

судя по формулам ничем!


смущает! почему нельзя было сразу посчитать по формуле:

P(B|A) = P(B )/P(А )????

зачем нужна формула P(AB ) = P(A)*P(B|A), если ответ равен P(B )???

не понимаю!!!

Автор: malkolm 29.1.2012, 5:49

Ну так не всегда же B вложено в A.

Автор: samik 29.1.2012, 7:29

ясно! спасибо за объяснения!

у меня возник еще один вопрос! есть задача:

В доске имеются отверстия (ячейки) с координатами

(Хк, Уl)

k=1,2,...n
l=1,2,...m
На доску брошен шарик, который может попасть в одну из ячеек. Вероятности попадания шарика в каждую из ячеек приведены в таблице(таблицу я добавил отдельно)

Вычислить вероятность попадания шарика в ячейку с абциссой Хк

я даже не знаю с чего начать!


Эскизы прикрепленных изображений

Автор: malkolm 29.1.2012, 8:25

Наверное, следует выяснить в учебнике, как по таблице совместного распределения пары случайных величин находятся распределения каждой из этих случайных величин?

Автор: samik 29.1.2012, 9:23

прочитал в учебнике, что это двумерная случайная величина.

я думаю в моем случае нужно воспользоваться частным законом распределения случайной величины.

я сделал следующим образом:

Р(Хк)=Рк1+Рк2+...+Ркm.

на сколько я понял нужно просумировать все вероятности в к-том столбце от 1 до m.

прошу исправить меня если я в чем то не прав или не правильно понимаю!

Автор: malkolm 29.1.2012, 9:25

Правильно, правильно.

Автор: samik 29.1.2012, 10:11

извеняюсь за свою наглость! но у меня есть еще одни вопрос, требующий Вашего одобрения или замечаний.

условия задачи:

Вычислить центральный момент четвертого порядка для общего нормального распределения вероятностей.

я ее решил двумя способами но не знаю на сколько правильно! я изложу Вам основную идею, а Вы скажите на сколько я прав!

1 способ
функция нормального распределения: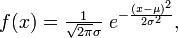


я расписал центальный момент четвертого порядка через начальные моменты


нашел математические ожидания для:

М(х), М(Х^2), M(x^3), M(x^4)
на сколько я понял это и есть начальные моменты:


далее подставил их в формулу:



2 способ

вычислил: М(х)
и по формуле представленной на картинке расчитал центральный момент. ответы решений совпали. хотелось бы услышать Ваше мнение по данной задаче.



Эскизы прикрепленных изображений

Автор: malkolm 29.1.2012, 11:21

Ну, если и в том, и в другом случае получилось три сигма в четвёртой, то верно.

Автор: samik 29.1.2012, 11:36

Так точно! в обоих случаях получилось три сигма в четвёртой!

Огромное спасибо Вам за помощь!

Автор: malkolm 29.1.2012, 11:42

На здоровье! Для интереса можно иметь в виду, что любой центральный момент чётного порядка 2k у того же нормального распределения равен (2k-1)!! = 1*3*...*(2k-1) - двойной факториал, т.е. произведение всех нечётных чисел, меньших 2k (да ещё умножить, разумеется, на сигма в степени 2k).

Автор: samik 29.1.2012, 14:51

Хорошо, буду иметь в виду! Спасибо еще раз за помощь и за интересную информацию!