Версия для печати темы

Автор: Ильмир 25.1.2012, 20:45

Здравствуйте.
Перезалил.

Пишу программу.

Программа должна нарисовать два круга. Радиусы известны.
Один круг маленький другой большой они вот должны касаться.


Проблема начинается с маленьким кругом. По идеи что бы его нарисовать нужно знать его координаты.

Координатам является центр окружности.

Координаты маленького круга по X найти легко, а вот по Y не как не могу додуматься. Спасибо за внимание.

Автор: tig81 26.1.2012, 8:59

Что делали?

Автор: Ильмир 26.1.2012, 12:09

Не понял вас.

Автор: tig81 26.1.2012, 12:56

Под "координатами маленького круга" подразумевается координаты его центра?

П.С. Дублировать темы не стоит. Пока устное предупреждение.

Автор: Ильмир 26.1.2012, 12:59

tig81 Понял. Больше такого не повториться.

Под "координатами маленького круга" подразумевается координаты его центра?

Именно.

Автор: Ильмир 28.1.2012, 11:49

tig81

Нашел координаты маленького круга.

x0=-r; y0=sqrt(r*r-R*R-2*R*x0-x0*x0);

формулу y0 можно еще упростить подставив место x0 "-r"

тогда получиться y0=sqrt(2*R*r-R*R)

решал с помощью системы уравнений окружности.



R, r , x0=-r известны

x,y, y0 не известны.

я взял случай в котором маленький круг, будет максимальной вылечены.
вот как тут. (Рисунок первый)


и взял их точки касания x=-R,y=0 и подставил.

Теперь x,y; типа известны. Вывел формулу и она рабочая. Нашел y0;


теперь мне нужна формула вычисляющая x,y;

так как радиусы произвольные. Значит нет у меня координатов точки касания.

Теоретически можно таким же образом найти x,y. Только тут две не известные координаты и все гораздо сложней. Теперь y0,x0,r,R известны; x,y не известны. 20 раз выводил формулу с нуля. И нет не работает

Автор: Dimka 28.1.2012, 13:41

Ничего не понял. Напишите яснее что должна делать Ваша программа.

Почему три рисунка?

Автор: Ильмир 28.1.2012, 14:38

Программа должна рисовать две окружности. Заданны произвольные радиусы. Условие что бы маленькая окружность касалась большого круга и диаметра как показано на рисунке. В рисунке показаны различные варианты радиуса окружностей для более лучшего понимания задачи.


По условию видно что r не может больше чем R/2, иначе не будет касания большой окружности и диаметра как показано на рисунке.



Для решения данной задачи нужно найти координаты маленькой окружности. Я вывел чудом формулу.помощью системы уравнений окружности.



Координаты большой окружности 0,0. То есть это начало координат. На декартовую систему координат нарисованная в самом низу не обращать внимания. потом легко будет перенести на нижнюю систему координат.

R, r , x0=-r известны

x,y, y0 не известны.


Так как не известны x,y;(координаты точки касания)
я решил взял случай в котором радиус маленькой окружности будет максимальной величины.
То есть r=R/2.
вот как тут. (Рисунок первый)



и взял их точки касания. Не трудно заметить что они будет равны x=-R,y=0 и подставил в уравнение.

Теперь x,y; типа известны. Вывел формулу и она оказалось рабочей для любых r<=R/2. Нашел y0;


Теперь координаты маленького круга известны. Они вычисляются по формуле x0=-r; y0=sqrt(2*R*r-R*R) И программа рисует окружности как надо


Следующая поставленная задача состоит в нахождении x,y то есть координаты точки касания окружностей.

Теоретически можно таким же образом найти x,y. Только тут две не известные координаты и все гораздо сложней. Теперь y0,x0,r,R известны; x,y не известны. 20 раз выводил формулу с нуля. И нет не работает

Автор: Dimka 28.1.2012, 15:56

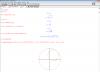
Вот.
Радиус большой окружности R и абсцисса точки касания на большой окружности x1 должны быть заданы. Дальше прога вычисляет уравнение малой окружности и строит его.


Эскизы прикрепленных изображений

Автор: Ильмир 28.1.2012, 16:14

Dimka

Я очень благодарен за помощь но вы к сожалению не так поняли.


мне известна формула нахождения координаты маленького круга. она равна x0=-r; y0=sqrt(2*R*r-R*R).

Но не известна формула нахождения координаты точки касания окружности.

Так как r и R произвольные. Только когда r=R/2 точка касания будет равна x=-R, y=0, а при других значениях r она будет равна другому значению.

Автор: Dimka 28.1.2012, 16:21

Какие величины изначально заданы (или вводятся клавы)?

Автор: Ильмир 28.1.2012, 16:24

r и R вводиться с клавы можно и так сказать.

Большего нечего.

Автор: Ильмир 28.1.2012, 16:44

Dimka я могу построить окружности как надо) так как у меня формула нахождения координат маленькой окружности есть.

Мне нужна формула координат касания окружностей. Для того что бы от этой точки нарисовать линию.

Автор: Dimka 28.1.2012, 16:50

Если R и r не связаны, а маленькая окружность должна находится внутри большой и касаться "обода" большой окружности, то точка касания должна быть задана, иначе комп не поймет в каком месте (вверху, внизу, справа, слева) размещать маленькую окружность.

Автор: Ильмир 28.1.2012, 17:07

Dimka

координаты маленькой окружности по x0 всегда будет x0=-r

по y0=sqrt(2*R*r-R*R) эту уже точно) Реализовано и работает. если выполняется условие r<=R/2 и это как раз что нам нужно.

Автор: Ильмир 29.1.2012, 3:37

Спасибо большое) решение найдено