Версия для печати темы
Нажмите сюда для просмотра этой темы в обычном формате
Образовательный студенческий форум _ Пределы _ lim(arctg(3x-6)/sqrt(1+sin(Пx)-1) при x->2
Автор: savedata 17.1.2011, 13:11
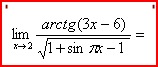
не могу понять зачем в знаменателе sqrt(1+sin(Пx)-1)
Автор: tig81 17.1.2011, 13:33
не могу понять зачем в знаменателе sqrt(1+sin(Пx)-1)
Ну условие такое. Или в чем вопрос?
Автор: savedata 17.1.2011, 13:37
условие
Автор: tig81 17.1.2011, 13:44
условие
а... наверное, все же не поняла, что вы хотели спросить, но наверное, вы не понимаете, почему 1 и -1? Т.к. если свести подобные, то получим 0?
Автор: savedata 17.1.2011, 13:57
ну если свести то 0, но тогда зачем так откровенно в задачнике написана формула?
в итоге тогда получается lim arctg(3x-6)/sinПx при x->2
используем эквивалентность бесконечно малых =>
lim (3x-6)/Пx при x->2; =(3*2-6)/2П=0/2П=0
верно?
Автор: tig81 17.1.2011, 14:00
ну если свести то 0, но тогда зачем так откровенно в задачнике написана формула?
Это вопрос ко мне? ИЛи он адресован авторам задачника, а это мысли вслух?
Скобки нигде не потеряны?
ну да
lim (3x-6)/Пx при x->2; =(3*2-6)/2П=0/2П=0
верно?
Эквивалентные бесконечно малые можно использовать, когда х->0, а у вас к 2.
Автор: savedata 17.1.2011, 14:14
точно.. а тогда как быть
Автор: tig81 17.1.2011, 14:15
точно.. а тогда как быть
Сделать замену так, чтобы новая переменная к 0 стремилась.
Автор: savedata 17.1.2011, 14:28
=lim arctg(3(x+2)-6)/(1+sin(П(x+2))-1) при x->0
=lim arctg(3x+6-6)/(1+sin(2П+Пx)-1)= lim arctg(3x)/sinПx при x->0
ЭБМ
=lim 3x/Пx=3/П
Автор: tig81 17.1.2011, 14:32
=lim arctg(3(x+2)-6)/(1+sin(П(x+2))-1) при x->0
=lim arctg(3x+6-6)/(1+sin(2П+Пx)-1)= lim arctg(3x)/sinПx при x->0
ЭБМ
=lim 3x/Пx=3/П
А какую замену делали? Просто получилось х на х заменили.
в знаменателе 1 надо было убрать.
А так похоже на правду.
Автор: savedata 17.1.2011, 14:34
x заменил на (x+2), единицы в знаменателе убрать, в смысле привести подобные?
Спасибо) по-моему получилось
А Вы могли бы мне еще вот в этой теме помочь? http://www.prepody.ru/topic12230.html?pid=69155&st=0&#entry69155
Автор: savedata 17.1.2011, 14:55
корень потерял...
=lim arctg(3(x+2)-6)/(1+sin(П(x+2))-1)^1/2 при x->0
=lim arctg(3x+6-6)/(1+sin(2П+Пx)-1)^1/2= lim arctg(3x)/(1+sinПx-1)^(1/2) при x->0
тогда lim (arctg(3x)*(1-(sinПx-1))^1/2)/(1-(1-2sinПx+(sinПx)^2))^1/2=
lim (arctg(3x)*(2-sinПx)^1/2)/(sinПx(2-sinПx))^1/2
ЭБМ
=lim (3x*(2-x)^1/2)/(x(2-x))^1/2=lim (((9x^2*(2-x))/(x(2-x)))^1/2=lim (9x)^1/2 при x->0
=0
Автор: tig81 17.1.2011, 14:56
x заменил на (x+2),
Ну обычно разные буковки пишутся, а то можно запутаться.
Ну да, там же 0, зачем их за собой таскать?
Пожалуйста, это хорошо.
Автор: savedata 17.1.2011, 15:17
=lim arctg(3(x+2)-6)/(1+sin(П(x+2))-1)^1/2 при x->0
вообщем вот, помучился, сделал в удобочитаемом виде

так правильно?
Автор: tig81 17.1.2011, 15:28
вообщем вот, помучился, сделал в удобочитаемом виде

так правильно?
А почему синус с 1 в скобках? 1 аргумент синуса?
Автор: savedata 17.1.2011, 15:41
в задачнике задание выглядит так: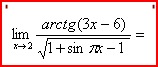
я просто (1+sinПx-1) разбил на пары (a+b ) и домножил на (a-b ) где a=1, b=sinПx-1
Автор: tig81 17.1.2011, 16:28
в задачнике задание выглядит так:
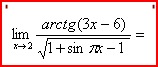
я просто (1+sinПx-1) разбил на пары (a+b ) и домножил на (a-b ) где a=1, b=sinПx-1
Что-то вы такое страшное сделали.
В знаменателе под корнем 1 убрать (т.е. свести подобные), затем замена x-2=t, затем эквивалентные бесконечно малые.
Автор: savedata 17.1.2011, 16:34
блин так реально проще))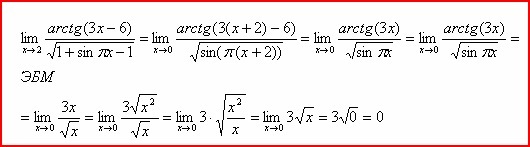
я не ищу легких путей) хотя суть та же)
Автор: Тролль 17.1.2011, 18:00
Лучше не писать x = (x^2)^(1/2), потому что (x^2)^(1/2) = |x|, а не х. Можно во второй строке второе и третье выражение вообще опустить.
Автор: savedata 18.1.2011, 11:42
учту на будущее
Русская версия Invision Power Board (http://www.invisionboard.com)
© Invision Power Services (http://www.invisionpower.com)
