Версия для печати темы

Автор: Резеда 10.1.2011, 18:36

Исследовать функцию и построить график

Подскажите пожалуйста, правильно ли я начала решать???

g(x) = (2x^2+x+1)*e^(1-x)

Решение:

1. Область определения Д (у) = (-бесконечн, + бесконечн)

2. ф-я ни четная, ни нечетная
у(-х) = (2(-х):2-х+1)*е^(1+x)=(2x^2-x+1)*e^(1+x)

3. Ф-я не явл периодичн.

4. Интервалы возрастания и убывания
производная у = e^(1-x) * (2x^2+5x+2)
производная у=0, при х=-2

Функция возрастает при х (-бесконеч;-2)
убывает при х (-2; +бесконеч)

5. Выпуклость и вогнутость кривой
у" = е^(1-x) * (2x^2+9x+7)
у" = 0 при х=-1

х (-бесконечн;-1) : у">0 - кривая вогнута
х (-3; + бесконечн) : у"<0 - кривая выпукла

(-1; 1/е)

Автор: Тролль 10.1.2011, 18:45

Производная неправильно найдена.

Автор: Резеда 10.1.2011, 18:54

спасибо, а подскажите пожалуйста в чем ошибка?
я производную обозначила значком ",
думаю что ошибка в вычислении производной от (e^(1-x))"


у" = (2x^2+x+1)"*e^(1-x) + (e^(1-x))" * (2x^2+x+1) =

e^(1-x) *(4x+1+2x^2+x+1) = e^(1-x) * (2x^2+5x+2)

Автор: Тролль 10.1.2011, 19:09

Производная e^(1 - x) равна -e^(1 - x)

Автор: Резеда 11.1.2011, 14:44

спасибо большое, сейчас буду дальше решать

Автор: Резеда 11.1.2011, 16:31

у меня получилось e^(1-x) * (3x-2x^2)
производная у=0, при х=0,
функция возрастает при х (-бесконечн,0)
функция убывает при х (0, + бесконечн)
точка максимума (0;2,7)
5. у"=(e^(1-x))" *(3x-2x^2) + e^(1-x) * (3x-2x^2)" = e^(1-x) * (2x^2-7x+3)
у"=0, при х=3
точка перегиба (3;1/е)

6. асимптоты
а) вертикальн: отсутствуют, т.к. функция всюду непрерывна
б) наклонные у= kx+b
lim(x стремящ к +- бесконечности) f(x) /x = k
lim(x стремящ к +- бесконечности) [f(x)-k*x]= b
k= - lim (x стремящ к -бесконечн) ((2x^2+x+1)* * e^(1-x)) / x = 0
k= - lim (x стремящ к +бесконечн) ((2x^2+x+1)* * e^(1-x)) / x = - бесконечн
b= - lim (x стремящ к -бесконечн) (2x^2+x+1) * e^(1-x) = 0
y=0 - наклонная (горизонт) асимпота

7. график


Подскажите правильно или нет?


в п.5 забыла написать:
х (-бесконеч,3) у">0 кривая вогнута
х (3;+бесконеч,3) у"<0 кривая выпукла
точка максимума (0; 2,7)

Автор: Тролль 12.1.2011, 8:38

Пока нет, экстремума два, а не один.

Автор: Резеда 13.1.2011, 16:46

надо найти еще точку минимума?

Автор: Тролль 14.1.2011, 6:01

Уравнение y' = 0 имеет два решения.

Автор: Резеда 14.1.2011, 17:39

y' = 0 при x=0 и x=1 ???

Автор: Тролль 14.1.2011, 17:46

Нет конечно.

Автор: Резеда 14.1.2011, 18:11

подскажите пожалуйста....

Автор: Резеда 14.1.2011, 18:28

Отсканировала свое решение, посмотрите пожалуйста... подскажите где ошибки


Мне подсказали. что:
4. две подозрительные на экстремум точки: x=0 и x=1.5 , т.е. производная функции равна 0 в этих двух точках.
5. аналогично, две точки перегиба x=3 и x=1/2
6. при стремлении к +бесконечности предел будет равен 0, а при стремл х к - бесконечности равен +бесконечность
примерный график, только я не совсем его поняла:

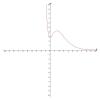
Автор: Тролль 14.1.2011, 18:48

y' = e^(1-x) * (3x-2x^2)
y' = 0 => e^(1 - x) * (3x - 2x^2) = 0
3x - 2x^2 = 0
x * (3 - 2x) = 0
x1 = 0 или 3 - 2x = 0 => x2 = 3/2
Исправляйте решение, будем дальше смотреть.

Автор: Резеда 14.1.2011, 19:07

5) y' = 0 => e^(1 - x) * (2x^2 - 7x +3) = 0
2x^2 - 7x +3= 0
(x-3) * (2x - 1) = 0
x1 = 3 или 2x - 1 = 0 => x2 = 1/2

а вот что дальше делать незнаюю...

Автор: Тролль 14.1.2011, 19:47

Сначала с y' закончите. Где будет возрастание и убывание, определите знаки.
Получаем две точки перегиба, находим, какие знаки принимает y'' на интервалах.

Автор: Резеда 15.1.2011, 4:56

4) y' (-бесконечн;0) (0;1,5) (1,5;+бесконечн)

при х (-бесконечн;0) функция убывает,
при х (0;1,5) функция возрастает,
при х (1,5;+бесконечн) функция убывает

при х=0 y' =0, у=2,7
при х=1,5 y' =0, у=4,3

5) точки перегиба х=3 и х=1/2

y'' (-бесконечн;1/2)(1/2;3)(3;+бесконечн)

при х (-бесконечн;1/2) кривая вогнута,
при х (1/2;3) кривая выпукла,
при х (3;+бесконечн) кривая вогнута

подскажите ПОЖАЛУЙСТА правильно или нет?

Автор: Тролль 15.1.2011, 7:55

при х = 1,5 y = 4,2
Остальное правильно.
Осталось найти асимптоты.

Автор: Резеда 15.1.2011, 13:38

6. Асимптоты
а) вертикальная отстутствует, т.к. функция всюду непрерывна
б) наклонные y=kx+b
lim x->+- бесконечн = k
lim x->+- бесконечн [f(x) - k*x] = b
k= - lim x-> - бесконечн [(2x^2 +x +1) * e^1-x] / x = бесконечн
k= - lim x-> + бесконечн [(2x^2 +x +1) * e^1-x] / x = 0
b = - lim x-> - бесконечн (2x^2 +x +1) * e^1-x = 0
y=0 горизонтальная асимптота

Автор: Тролль 15.1.2011, 13:41

Да, причем график стремится к асимптоте при x -> +00

Автор: Резеда 15.1.2011, 14:04

спасибо
это мне в конце дописать нужно??? получается на этом задание решено? график правильный?

Автор: Тролль 15.1.2011, 14:08

Вертикальной асимптоты нет.
Горизонтальная асимптота находится так:
lim (x->-00) y - здесь предел бесконечность
lim (x->+00) y = 0 => y = 0 - горизонтальная асимптота.
А наклонных нет, так как lim (x->00) y/x равен бесконечности.

График правильный.

Автор: Резеда 15.1.2011, 14:36

Получается мне вместо:
6. Асимптоты
а) вертикальная отстутствует, т.к. функция всюду непрерывна
б) наклонные y=kx+b
lim x->+- бесконечн = k
lim x->+- бесконечн [f(x) - k*x] = b
k= - lim x-> - бесконечн [(2x^2 +x +1) * e^1-x] / x = бесконечн
k= - lim x-> + бесконечн [(2x^2 +x +1) * e^1-x] / x = 0
b = - lim x-> - бесконечн (2x^2 +x +1) * e^1-x = 0
y=0 горизонтальная асимптота

НАДО НАПИСАТЬ:

Вертикальной асимптоты нет.
Горизонтальная асимптота:
lim (x->-00) y - здесь предел бесконечность
lim (x->+00) y = 0 => y = 0 - горизонтальная асимптота.
А наклонных нет, так как lim (x->00) y/x равен бесконечности.

спасибо...

Автор: Тролль 15.1.2011, 15:23

Не совсем. а) можно оставить так, как у Вас.

Автор: Резеда 15.1.2011, 15:24

а б)? как у вас?

Автор: Тролль 15.1.2011, 15:34

Остальное да, только конечно надо расписать, а не писать просто словами, что предел равен бесконечности.

Автор: Резеда 15.1.2011, 15:48

б) наклонные y=kx+b
lim x->+- бесконечн = k
lim x->+- бесконечн [f(x) - k*x] = b
k= lim x-> - бесконечн [(2x^2 +x +1) * e^1-x] / x = бесконечн
k= lim x-> + бесконечн [(2x^2 +x +1) * e^1-x] / x = 0
b = lim x-> - бесконечн (2x^2 +x +1) * e^1-x = 0
y=0 горизонтальная асимптота
наклонных асимптот нет, так как lim (x->00) y/x равен бесконечности.
???

Автор: Тролль 15.1.2011, 15:51

Я имел в виду как у меня) Хотя можно оставить как у Вас.
Только нужно исправить: b мы находим при x->+00
И про наклонные асимптоты последнюю фразу можно уже не писать.

Автор: Резеда 15.1.2011, 15:58

СПАСИБО!!!!!!!
сейчас еще буду вторую функцию пытаться исследовать...

Автор: Резеда 16.1.2011, 20:49

есть еще одна функция на исследование...
если есть возможность ПОМОГИТЕ ПОЖАЛУЙСТА...
хотя бы в построении графика..

f(x)= (3x^2 - x^3) / 2

1. точек разрыва нет
пересечение с ох х=0, у=0
2. Функция ни четна, ни нечетна
3. Функция не явл периодич
4. Интервалы возрастания и убывания производная у = (x^3 - 9x^2 + 12x) / 4
производная у=0 при х=0 и х=3
х (-00; 0)(0;3)(3;+00) бесконечность обозначила 00
5. выпуклость и вогнутость у" = (-x^3 + 21x^2 -76x +48) / 16
у" = 0 -> -x^3 + 21x^2 -76x +48 = 0

А дальше незнаю...

Автор: Тролль 16.1.2011, 20:52

Пересечений с Ох больше, чем одна.
Производная неправильно найдена.

Автор: Резеда 16.1.2011, 21:16

Спасибо!!!
у = (x^3 - 9x^2 + 12x) / 4 непраильно найдена, не пойму где ошибка...

Автор: Тролль 16.1.2011, 21:17

Как находили производную?

Автор: Резеда 16.1.2011, 21:26

(3x^2 - x^3) / 2
у'= [(3x^2 - x^3)' * 2 - 2' * (3x^2 - x^3)] / 2^2 = [2 * (6x - 3x^2) - (3x^2 - x^3)] / 4 =
= [12x -6x^2 - 3x^2 + x^3] / 4= [x^3 -9x^2 +12x] /4 ???

Автор: Тролль 16.1.2011, 21:30

Слишком сложно. Это табличная производная. Да и в приведенном решении ошибка - неверно вычислена 2'.

Автор: Резеда 16.1.2011, 21:41

а как будет верна?? производная от числа разве не 1??

Автор: Тролль 16.1.2011, 21:43

Нет конечно.

Автор: Резеда 16.1.2011, 21:45

нулю ???

Автор: Тролль 16.1.2011, 21:49

Не гадайте. Посмотрите таблицу производных.

Автор: Резеда 17.1.2011, 10:49

Вот кое-что нарешала, посмотрите пожалуйста, только качество не очень получилось...





какие промежутки нужно брать?
и окончание как всегда не могу сделать, еще нужно график начертить...
А сдавать уже в среду надо...
Подскажите пожалуйста....

Автор: Тролль 17.1.2011, 11:44

Область определения неправильно нашли. И со значениями производной в 0 и 2 напутали.
А где промежутки выпуклости и вогнутости?

Автор: Резеда 17.1.2011, 12:05

Область определения - так и не пойму в чем ошибка... это в пункте 1 ???

"И со значениями производной в 0 и 2 напутали" производная при (0) = 0 и при (2) = 0
промежутки выпуклости и вогнутости (-00 ;1) у'' > 0
(1;+00) у'' < 0

Получается надо брать левую таблицу???

Автор: Тролль 17.1.2011, 15:27

Левую. Область определения какая?

Автор: Резеда 17.1.2011, 16:16

(-00;0) (0;2) (2;3) (3; +00) ???

Автор: Тролль 17.1.2011, 16:19

Нет. Что такое область определения?

Автор: Резеда 17.1.2011, 16:38

Область определения функции – это множество значений аргумента, при которых функция задана, определена.
(-00; +00)

Автор: Тролль 17.1.2011, 17:31

Вот, теперь правильно.
Теперь всё решение напишите.

Автор: Резеда 17.1.2011, 17:48

f(x)= (3x^2 - x^3) / 2

1. область опред (-00; +00)

2. Функция ни четна, ни нечетна f(-x) = (3x^2 + x^3) / 2

3. Функция не явл периодич

4. Интервалы возрастания и убывания производная у = (6x - 3x^2) / 2 = [ 3x * (2 - x) ] / 2
производная у=0 при х=0 и х=2
х (-00; 0)(0;2)(2;+00) бесконечность обозначила 00

на промежутке (-00; 0) f ' (x) = "-" , f(x) - убывает
при х=0 f ' (x) = 0 , f(x) - не существует
на промежутке (0;2) f ' (x) = "+" , f(x) - возрастает
при х=2 f ' (x) = 0 , f(x) - не существует
на промежутке (2;+00) f ' (x) = "-" , f(x) - убывает

5. выпуклость и вогнутость у" = 3-3х = 3 * (1-х)
у" = 0 -> 3*(1-х)= 0 х=1
(-00;1) (1;+00)
(-00;1) у" >0 функция выпукла
(1;+00) у" <0 функция вогнута

6. асимптота
а) вертикальная х=0, х=3
б) наклонная у= kx + b
lim x-> +-00 f(x) / (x) = k
k = -lim x-> -00 [3x^2 - x^3] /2 = +00
k = -lim x-> +00 [3x^2 - x^3] /2 = 0
b = lim x-> +00 [3x^2 - x^3] /2 = ...

еще график нужен...

Автор: Тролль 17.1.2011, 17:57

А промежутки, где y > 0 и y < 0 не нужно искать?
Почему при x = 0 и x = 2 функция не существует??
Если y''>0, то функция наоборот вогнута. Тоже для y''<0.
Вертикальных асимптот нет, так как функция всюду непрерывна.
Асимптоты: не надо разбивать на два случая: x->-00 и x>+00
Для случая x->+00 неправильно найдено k.

Автор: Резеда 17.1.2011, 18:15

f(x)= (3x^2 - x^3) / 2

1. область опред (-00; +00)

y > 0 при х (-00 ; 3) и y < 0 при х (4;+00)

2. Функция ни четна, ни нечетна f(-x) = (3x^2 + x^3) / 2

3. Функция не явл периодич

4. Интервалы возрастания и убывания производная у = (6x - 3x^2) / 2 = [ 3x * (2 - x) ] / 2
производная у=0 при х=0 и х=2
х (-00; 0)(0;2)(2;+00) бесконечность обозначила 00

на промежутке (-00; 0) f ' (x) = "-" , f(x) - убывает
при х=0 f ' (x) = 0 , f(x) =0
на промежутке (0;2) f ' (x) = "+" , f(x) - возрастает
при х=2 f ' (x) = 0 , f(x) =0
на промежутке (2;+00) f ' (x) = "-" , f(x) - убывает

5. выпуклость и вогнутость у" = 3-3х = 3 * (1-х)
у" = 0 -> 3*(1-х)= 0 х=1
(-00;1) (1;+00)
(-00;1) у" >0 функция вогнута
(1;+00) у" <0 функция выпукла

6. асимптота
а) вертикальная не сущ, т.к. функция всюду непрерывна
б) наклонная у= kx + b
lim x-> +-00 f(x) / (x) = k
k = -lim x-> -00 [3x^2 - x^3] /2 = +00
k = -lim x-> +00 [3x^2 - x^3] /2 = -00
b = lim x-> +00 [3x^2 - x^3] /2 = ...

еще график нужен...

Автор: Тролль 17.1.2011, 18:20

1. Промежутки, где y > 0 и y < 0 неправильны.
4. f(0) = 0, а f(2) не равно 0
6. Если k равно бесконечности, то про b вообще не надо говорить.

Автор: Резеда 17.1.2011, 18:35

1. у> 0 при х (-00;0) (0;3) у<0 при х (3;+00)
4. f(2) = 2
6. b убираю совсем
так? подскажите пожалуйста...

Автор: Тролль 17.1.2011, 18:38

Да, тогда всё правильно. Осталось график построить.

Автор: Резеда 17.1.2011, 18:42

спасибо ОГРОМНЕЙШЕЕ!!!
2 точки (0;0) и (2;2)
на промежутке от -00 до 0 убывает, от 0 до 2 возрастает, от 2 до +00 опять убывает??? если есть возможность у Вас скиньте пожалуйста график...

Автор: tig81 17.1.2011, 18:43

Скачайте бесплатную программу Advanced Grapher

Автор: Резеда 17.1.2011, 18:52

Спасибо!!! сейчас попробую..

Автор: tig81 17.1.2011, 18:54

Пожалуйста!

Автор: Резеда 18.1.2011, 8:16

Хотела отправить решение для того, чтобы посмотрели правильность, а объем файла намного больше допустимого (((

Автор: Тролль 18.1.2011, 8:26

Построили график в программе? Проверьте полученные Вами пункты -тоже на графике?

Автор: tig81 18.1.2011, 8:30

Залейте картинку на www.radikal.ru или www.radikal.ua и сюда вторую ссылку.

Автор: Резеда 18.1.2011, 9:03

http://s51.radikal.ru/i134/1101/26/6b826171c6c7.jpg
и
http://s40.radikal.ru/i089/1101/ee/f990152d4394.jpg

Автор: Тролль 18.1.2011, 9:11

1. Не найдены интервалы вогнутости и выпуклости.
Почему при вычислении k перед пределом стоит минус??
При х->+00 график должен стремиться к 0.
2. Надо написать, что наклонных и горизонтальных асимптот нет.
График неправильный.

Автор: Резеда 18.1.2011, 9:55

1. http://s014.radikal.ru/i327/1101/0c/93a42c427110.jpg
2. http://s010.radikal.ru/i311/1101/70/f29a10255a03.jpg

Автор: Тролль 18.1.2011, 9:59

1. Интервалы вогнутости и выпуклости неправильные.
2. Да, там не правильно.

Автор: Резеда 18.1.2011, 10:18

1. у" > 0 при (-00 ; 1) ( 3 ; +00)
у" < 0 при ( 1 ; 3 )
2. http://s003.radikal.ru/i204/1101/1c/9938d8935611.jpg

Автор: Тролль 18.1.2011, 10:31

1. Нет.
2. Нет.

Автор: Резеда 18.1.2011, 10:51

Подскажите пожалуйста... а то мне еще 3 задачи нужно решить, а сдавать уже завтра надо... ПОЖАЛУЙСТА...

Автор: Тролль 18.1.2011, 11:08

1. Где точки перегиба? Они разбивают ось Ох на нужные интервалы.
2. Стройте график по пунктам. Или используйте программу.

Автор: Резеда 18.1.2011, 11:35

1. у" > 0 при (-00 ; 1/2) ( 3 ; +00)
у" < 0 при ( 1/2 ; 3 )

Автор: Тролль 18.1.2011, 11:37

Да, теперь правильно.

Автор: Резеда 18.1.2011, 11:39

наконец-то, я наверное вас замучила... извините если что... теперь 2 график нужен, я так поняла мне надо промежуток от точки (2 ; 2) подправить?

Автор: Тролль 18.1.2011, 11:42

Постройте его с помощью программы. У Вас же получилось, что нет асимптот, почему они вдруг возникли?

Автор: Резеда 18.1.2011, 15:35

правильно? подскажите пожалуйста...

Автор: Тролль 18.1.2011, 15:41

Да, правильно.

Автор: Резеда 18.1.2011, 16:41

Спасибо Вам огромное!!!