Версия для печати темы
Нажмите сюда для просмотра этой темы в обычном формате
Образовательный студенческий форум _ Геометрия _ Помогите построить сечения
Автор: Koketka 20.12.2010, 13:28
Задание:
1 серия: Построить сечение многогранника плоскостью, заданной тремя точками
2 серия: Построить сечение многогранника плоскостью, проходящей через две данные точки, параллельно заданной прямой.
3 серия: Построить сечение многогранника плоскостью, проходящей через данную точку, параллельно заданной плоскости
Эскизы прикрепленных изображений![]()
Автор: tig81 20.12.2010, 13:57
Что делали? Что не получается? Почитайте про метод следов.
Автор: Koketka 10.1.2011, 7:51
Проверьте пожалуйста правильность моего решения (дана диагональ куба B1D и точки F, G). Надо построить сечение плоскостью, проходящей через две данные точки параллельно заданной прямой.
Пусть α – плоскость сечения
1. B1C1||AD, FεB1C1, B1εB1C1, DεAD, EεAD, DE=B1F, следовательно, B1FED – параллелограмм, FE||B1D
2. Eε(ABC), Gε(ABC), следовательно, GE – след α на плоскости (ABC)
3. Прямая EG пересекает прямую DC в точке K, DC||A1B1, строим B1L=DK, DKLB1 – параллелограмм по построению
4. Lε(A1B1C1), Fε(A1B1C1), следовательно, LF – след α на плоскости (A1B1C1)
5. Прямая LF пересекает прямую в точке M, MεD1C1, Mε(DCC1), Kε(DCC1), следовательно, MK – след плоскости α на плоскости (DCC1)
6. Lε(A1B1B), Gε(A1B1B), следовательно, LG – след α на плоскости (A1B1B)
7. Прямая LG пересекает прямую B1B в точке P, Pε(BCC1), Fε(BCC1), следовательно, PF – след α на плоскости (BCC1)
8. GPFMK – искомое сечение
Преподаватель задал мне такой вопрос: диагональ куба B1D и точка F образует плоскость, что это за плоскость? И почему точка Е оказалась именно в нижней грани куба (ABC)? Помогите мне объяснить
Эскизы прикрепленных изображений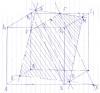
Русская версия Invision Power Board (http://www.invisionboard.com)
© Invision Power Services (http://www.invisionpower.com)