Версия для печати темы
Нажмите сюда для просмотра этой темы в обычном формате
Образовательный студенческий форум _ Линейная алгебра и аналитическая геометрия _ Собственные числа\вектора
Автор: fatalisk 18.12.2010, 21:31
Найти собственные числа и собственные вектора линейного оператора с матрицей А
2 -1 1
А=-1 2 1
0 0 1
Сделано: нашел собственные числа лямбда1=1 и лямбда2=2, далее как делать не понятно.
рассматриваем случай для Л1=1, да? получается красивая матрица
1 -1 1
0 0 0
0 0 0
И все! финиш! Посмотрел пример, там красота: Очевидно, что rang=1, следовательно, число собственных векторов для l1=1 равно n-rang=2. Найдем их" и ответ! Все очевидно и не понятно![]() Объясните плиз.
Объясните плиз.
воо, нашел еще пример(http://www.reshebnik.ru/solutions/10/9) в котором не понятно это- 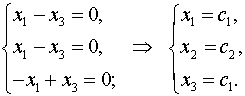
как получилась первая система ясно, но вот дальнейший переход...
Автор: Hottabych 18.12.2010, 21:58
получается красивая матрица
1 -1 1
0 0 0
0 0 0
И все! финиш!
x-y+z=0 => x=y-z
y=C1,z=C2,x=C1-C2
Автор: fatalisk 18.12.2010, 22:12
x-y+z=0 => x=y-z
y=C1,z=C2,x=C1-C2
первая строчка - очевидно
вторая - и что нам это дает? к сожалению не наталкивает на решение
Автор: Тролль 19.12.2010, 8:32
Теперь выбираем С1 и С2.
Берем C1 = 0, C2 = 1
А затем C1 = 1, C2 = 0
Получаем векторы (-1;0;1) и (1;1;0)
Автор: fatalisk 19.12.2010, 9:43
Теперь выбираем С1 и С2.
Берем C1 = 0, C2 = 1
А затем C1 = 1, C2 = 0
Получаем векторы (-1;0;1) и (1;1;0)
Теперь вроде понятно, спасибо.
Русская версия Invision Power Board (http://www.invisionboard.com)
© Invision Power Services (http://www.invisionpower.com)
