Версия для печати темы

Автор: coffe 7.12.2010, 18:04

Здравствуйте... подскажите пожалуйста..


A B C D :

(2,4,5) (1,-2,3) (-1,-2,4) (2,-1,7) 2 : 3

в) скалярное произведение векторов a и b:

a*b= 2*1+4*(-2)+5*3=2-8+15=9 Верно???

А как найти длину вектора?

Автор: tig81 7.12.2010, 18:40

Напишите полное условие.
Про длину вектора посмотрите либо в гугле, либо в конспекте.

Автор: coffe 7.12.2010, 18:45

ищу... чет пока нужного не нашла.. конспекта нет

Полное условие:


Эскизы прикрепленных изображений

Автор: Dimka 7.12.2010, 20:20

Корень квадратный из суммы квадратов координат вектора

Автор: Harch 8.12.2010, 12:04

Ну, это в евлидовом пространстве а так корень из скалярного произведения на себя

Автор: coffe 8.12.2010, 16:17

все равно не поняла

Автор: coffe 8.12.2010, 16:53

я начала с самого начала... нахожу а ... посмотрите пожалуйста, я правильно начала или нет??


Эскизы прикрепленных изображений

Автор: coffe 8.12.2010, 17:20

продолжение...


Эскизы прикрепленных изображений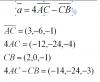

Автор: Тролль 8.12.2010, 17:58

Опечатка в самом начале: Надо AC = (-3;-6;-1)
Остальное всё верно.

Автор: coffe 8.12.2010, 18:19

спасибо)) а как мне теперь координаты вектора а найти??

Автор: Тролль 8.12.2010, 21:01

Так он же уже найден.

Автор: Dimka 9.12.2010, 5:49

координаты вектора a

a=4AC-CB=(-14,-24,-3)

Длина вектора a

|a|=sqrt(14^2+24^2+3^2)=sqrt(781)

Автор: coffe 9.12.2010, 15:14

спасибо..большое))))

Автор: Harch 9.12.2010, 15:51

Пожалуйста.