Версия для печати темы

Автор: OomphRt 4.12.2010, 18:37

Помогите решать, корни нашёл а вот дальше незнаю как
http://img.pixs.ru/storage/6/6/4/0412201008_9636658_1309664.jpg

Автор: tig81 4.12.2010, 18:41

неправильно нашли

Посмотрите http://www.reshebnik.ru/solutions/5/12/ примеры.

Автор: OomphRt 4.12.2010, 18:57

таки получаться вроде?
http://radikal.ua

Автор: tig81 4.12.2010, 19:09

Практические:
yo=C1e^(2x)+C2e^(-2x)

Автор: OomphRt 4.12.2010, 19:13

Забыл поставить индекс нужный,
вот во всех уравнениях правая часть на примерах в стиле "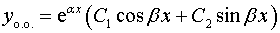
А как у меня выглядит будет, нигде не могу найти

Автор: tig81 4.12.2010, 19:23

У вас частное решение запишется в виде суммы двух: yч=yч1+yч2, где уч1=Ae^(2x)*x, yч2=Bcos2x+Csin2x

Автор: OomphRt 4.12.2010, 21:02

я чёто не допер как мы так корни получили?
там же
y^2-4y=0

а не y^2-4=0

Автор: Тролль 4.12.2010, 21:32

Там y^2 - 4 = 0

Автор: OomphRt 4.12.2010, 22:59

ну может я так коряво пишу, но там y^2-4y=0

Автор: tig81 5.12.2010, 6:57

Там, это где?

Автор: OomphRt 5.12.2010, 10:14

Эм, ну в частной производной высшего порядка

Автор: tig81 5.12.2010, 10:32

Где у вас здесь частные производные?

Автор: OomphRt 5.12.2010, 10:44

да я спутал тематику, в дифф уравнении.
там корни 4 и 0
y^2-4y=0

Автор: tig81 5.12.2010, 10:52

Вам же уже неоднократно писали, что характеристическое уравнение не такое.

Автор: OomphRt 5.12.2010, 10:54

Спасибо, понял

Автор: tig81 5.12.2010, 10:58

Автор: OomphRt 6.12.2010, 16:03

Самое интересное решал с корнями 4 и 0
и мне препод сказал, правильно_
вроде как решил

Автор: Тролль 6.12.2010, 17:29

В данном уравнении корни действительно равны 0 и 4, а в первом уравнении 2 и -2.
Всё верно, осталось ответ записать.

Автор: tig81 6.12.2010, 17:49

Поддерживаю. Сравните второе слагаемое в начальном и в последнем посте.

Автор: OomphRt 7.12.2010, 5:20

Да да записал, на обороте и сдал, в четверг должен узнать