Версия для печати темы

Автор: OomphRt 4.12.2010, 18:28

В общем контру делаю , в чём ошибка, препод не обяснил, и помогите дорешить
http://img.pixs.ru/storage/6/1/2/0212201007_4643187_1309612.jpg
http://radikal.ua

Автор: tig81 4.12.2010, 18:39

Частная производная по х найдена неверно. Вам это преподаватель и подчеркнул.

Автор: OomphRt 4.12.2010, 18:40

Можете помочь решить, чёт не дорубаю как ошибся

Автор: tig81 4.12.2010, 18:44

Чему равна производная выражения х/у по переменной х?

Автор: OomphRt 4.12.2010, 18:49

получиться вроде 1/y

Автор: tig81 4.12.2010, 19:01

А у вас на листике, что написано?

Автор: OomphRt 4.12.2010, 19:33

Вроде прорешал, можешь проверить, накосячил или нет?

Автор: tig81 4.12.2010, 19:40

1. смешанная производная найдена неверно.
2. Производная по у неправильно.

Автор: OomphRt 4.12.2010, 19:56

Вроде исправил,глянь правильно?, а вторая по "x" правильно была?)

Автор: Тролль 4.12.2010, 21:30

dz/dx правильно
d^2 z/dxdy не верно
d^2 z/dx^2 почему два раза e^(xy)?
dz/dy тоже не верно

Автор: OomphRt 4.12.2010, 23:06

всё подрубил)


Почему? можете помочь а то я уже не врубаю где же я ошибаюсь

http://img.pixs.ru/storage/3/1/8/0512201009_6944560_1311318.jpg

Автор: Тролль 5.12.2010, 7:49

d^2 z/dx^2 верно, но можно упростить, сократив y.
Двойка в dx^2 должна стоять не внизу, а вверху.
dz/dy все равно неправильно.
Производная x/y по производной y равна не х, а -x/y^2.

Автор: Harch 5.12.2010, 9:30

кгхм... повежливее пожалуйста, тут интеллигентные люди Вам помогают.

Автор: OomphRt 5.12.2010, 10:52

Да конечно, извеняюсь.
А смешанную то правильно нашёл?

Автор: tig81 5.12.2010, 10:55

Нет, второе слагаемое не такое. Чему равна производная выражения e^(xy)/y по у?

Автор: OomphRt 5.12.2010, 11:05

(e^(xy)-x*e^(xy)*y)/(y^2)
Так вроде?

Автор: tig81 5.12.2010, 11:08

нет
(u/v)'=(u'v-uv')/v^2

Автор: OomphRt 5.12.2010, 11:33

Вроде нашёл, будьте добры помогите со второй производной по y
Ну не как не найти

Автор: tig81 5.12.2010, 11:36

1. В смешанной производной откуда 2х взялось?
2. Расскажите, какие правила применяли для нахождения второй по у.

Автор: OomphRt 5.12.2010, 11:42

там X*X я записал как 2x
или это имеет значение как записать



Изначально :
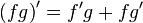
А для (-x/y^2) вроде как

Автор: tig81 5.12.2010, 11:47

х*х=x^2
2x=x+x

Автор: Тролль 5.12.2010, 11:48

x * x равно не 2x, а x^2
e^(xy) + e^(xy) = 2 * e^(xy)
Осталось d^2 z/dy^2 найти правильно.

Автор: OomphRt 5.12.2010, 12:08

Вроде решил
посмотрите

Автор: tig81 5.12.2010, 13:57

Вторая производная по у, первые два слагаемых: что и по какой переменной дифференцировали?

Автор: OomphRt 5.12.2010, 14:08

Если не так то будьте добры можете обьяснить как получаеться

Автор: tig81 5.12.2010, 14:30

Распишите подробно, как находили производную.

Автор: OomphRt 5.12.2010, 14:41

ну как бы uv=u'v+uv'
Я веди снизу перерешал

Автор: OomphRt 5.12.2010, 19:39

Не могли бы помочь с этой производной. по dy, а то завтра сдать желательно

Автор: tig81 5.12.2010, 19:47

(x^2*e^(xy)/y)'=x^2(e^(xy)/y)'=...
Чему равна производная по у?

Автор: OomphRt 5.12.2010, 20:41

Вроде так

Автор: tig81 5.12.2010, 21:19

во второй производной по у в последнем слагаемом дробь неверно:
dz/dy=x^2*e^(xy)/y-xe^(xy)/y^2
d^2z/dy^2=x^2*[xe^(xy)*y-e^(xy)]/y^2-x*[xe^(xy)*y^2-e^(xy)*2y]/y^4
Вроде так

Автор: OomphRt 5.12.2010, 22:01

Спасибо, завтра узнаем)

Автор: tig81 5.12.2010, 22:02