Версия для печати темы
Нажмите сюда для просмотра этой темы в обычном формате
Образовательный студенческий форум _ Дифференциальные уравнения _ (x-1)*y'+y=(x^2) -1
Автор: граф Монте-Кристо 29.5.2010, 15:23
Что не получается? Где свои идеи?
Автор: tig81 29.5.2010, 15:47
Вот как я решил (но я сомневаюсь , что правильно):
Четвертая строчка: у=С(х-1)
Далее объясните, что делали.
Автор: граф Монте-Кристо 29.5.2010, 15:50
Минус потеряли во второй строчке.
Автор: huxxboxx 29.5.2010, 15:51
Я решил по подобию вот этого примера у вас на форуме http://www.prepody.ru/topic10033.html
Автор: huxxboxx 29.5.2010, 16:19
Вообщем сейчас заного решил , только вот я не пойму как находить y'=???(что и куда подставлять помогите)
Пока так: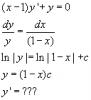
Автор: tig81 29.5.2010, 16:30
Минус потеряли во второй строчке.
Точно, пропустила.
Точно, пропустила.
В третьей строке перед логарифмом минус должен быть.
Тогда у=С/(1-х).
А зачем вам искать y', если вы ищите у?
П.С. Но это вы нашли решение однородного уравнения, но изначально в правой части стоит некоторая функция.
Автор: huxxboxx 29.5.2010, 16:34
поправил: 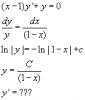
http://www.prepody.ru/topic10033.html -я пытаюсь решить пример по этой ссылке , вот только они там не расписали как нашли y'=....
Может я вообще неправильный метод решения выбрал? подскажите...
Автор: tig81 29.5.2010, 16:49
http://www.prepody.ru/topic10033.html -я пытаюсь решить пример по этой ссылке
y=(x/(1-x))*c
дальше полагала, сто с=c(x)
Это есть?
Цитата
вот только они там не расписали как нашли y'=....
Цитата
y`=c/((1-x)^2)+c`*x/(1-x)
Нашли производную от полученного решения однородного уравнения.
Автор: tig81 29.5.2010, 17:29
Вот что я получил :
Немного не так:
y=C(x)/(1-x)
y'=[C'*(1-x)-C*(1-x)']/(1-x)^2=[C'*(1-x)-C*(1-x)']/(x-1)^2
Теперь выражения для у и y' подставляйте в исходное дифференциальное уравнение и решайте его относительно С.
Автор: tig81 29.5.2010, 20:35
Вообщем в итоге решил подругому ,
ну можно и так.
Цитата
проверьте пожалуйста:
Не поняла как из того, что предположили v=v(x), получили выражение в пятой строке.
Посмотрите http://www.reshebnik.ru/solutions/5/4/ и оформите таким образом. А то немного накручено.
Автор: huxxboxx 30.5.2010, 13:14
tig81 , огромно человеческое спасибо вам за помощь...
Автор: tig81 30.5.2010, 14:11
Пожалуйста!
Русская версия Invision Power Board (http://www.invisionboard.com)
© Invision Power Services (http://www.invisionpower.com)