Версия для печати темы

Нажмите сюда для просмотра этой темы в обычном формате

Образовательный студенческий форум _ Теория вероятностей _ распределения немонотонной функции одного случайного аргумента

Автор: matan 16.5.2010, 12:19

по условию: случайная величина задана плотностью распределения f(x) на интервале (-inf;inf)
Y=cos(x); я предполагаю следующее решение: 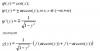Прикрепленное изображение

Автор: malkolm 16.5.2010, 13:03

Это вообще не решение. Что такое y=+- arccos(y) - уравнение на y?

Вы же в заголовке отметили, что функция cos(х) - немонотонная! Нет у неё обратной функции на всей прямой.

Ищите по определению функцию распределения Y.

Автор: matan 16.5.2010, 14:46

блин, и как это ?? вообще не пойму что именно нужно делать.

Автор: malkolm 16.5.2010, 18:54

Вы о чём? blink.gif
Перевожу:
Распределение случайной величины Х задано плотностью распределения f(x) на всей прямой. Случайная величина Y = cos(X). Требуется найти плотность распределения Y.

Предлагаю ТС как минимум начать вычислять функцию распределения. Задачи такой степени общности в заборостроительном институте не даются. Стало быть, ТС по определению должен обладать достаточными знаниями, чтобы хотя бы понимать условие.

Автор: Juliya 16.5.2010, 19:06

ой, проглядела Y... blush.gif

ps удалила свое сообщение, т.к. редактировать нельзя

Русская версия Invision Power Board (http://www.invisionboard.com)
© Invision Power Services (http://www.invisionpower.com)