Случайная величина Х подчинена нормальному закону распределения с нулевым математическим ожиданием. Вероятность попадания этой случайной величины в интервал (–2;2) равна 0,5705. Найти среднее квадратическое отклонение и плотность вероятности этой случайной величины.
Итак, формула есть
 куда я подставляю свои значения интервала х1 и х2 и также из условия мне дано, что всё это дело равно 0,5705
куда я подставляю свои значения интервала х1 и х2 и также из условия мне дано, что всё это дело равно 0,5705и вроде бы всё не так уж сложно, но я никак не могу понять как найти параметр в знаменателе моей гениальной формулы (дико стыдно, но я забыла как называется эта буква
как только я пойму это, можно будет смело находить плотность вероятности СВ из формулы
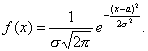
в общем, надеюсь на вашу помощь)
В условии Вам так же дано что математическое ожидание а=0
Тогда Ваш интервал (-2;2) это симметричный интервал
Р(-2;2)=2Р(0;2)=0,5705
Ну дальше все просто. Находите чему равно сигма и решаете задачу.
