Нахождение кратчайшего пути в трехмерной системе координат Опции

[champforgame]

Добрый день, уважаемые знатоки.

Есть трёхмерное пространство. В нем всегда располагаются два вектора. Необходимо создать кратчайший путь с помощью перпендикуляров . Я не знаю как выразится, но хотелось бы чтобы кратчайший путь состоял из отрезков точки которых находятся в ДВУМЕРНОМ пространстве.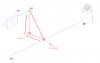


Случай первый ХОЧУ чтобы алгоритм выполнял такой случай так (скриншот 1):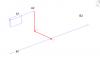

Вектор А1-А2
(X,Y,Z)
A1 (143,604, -106,206, 1,958)
A2 (145,010, -106,530, 1,958)
Вектор B1-B2
(X,Y,Z)
B1 (140,200, -108,156, -0,0656)
B2 (149,279, -110,252, -0,0656)

Случай второй ХОЧУ чтобы алгоритм выполнял такой случай так (скриншот 2):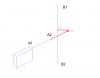


Вектор А1-А2
(X,Y,Z)
A1(143,6040 -120,821, 16,5740)
A2 (145,010, -121,1463, 16,5740)

Вектор B1-B2
(X,Y,Z)
B1 (146,274, -120,6302, 13,385)
B2 (146,274, -120,6302, 18,307)

Объясните пожалуйста:
1) Если есть алгоритмы, то как они называются и есть ли на них ссылки?
2) Я программирую на Python и хотелось бы программе объяснить за счет чего можно объяснить коду, чтобы он проделал все так как я показал в 1 и во втором случае (делает он у меня как на скрине "КАК НЕ НАДО"). Либо делает, но тогда работает он топорно.
3) Как бы вы решили этот вопрос

Заранее благодарю вас!

[champforgame]

UP



ИСХОДНЫЕ ДАННЫЕ
Имеется трехмерное пространство. В нем имеет прямоугольный объект (батарея радиатора), от него отходит труба, представляющая собой отрезок с точками А1-А2. Рядом с ними находится главный трубопровод под уклоном , представляет собой отрезок B1-B2. Координаты точке на картинке.
https://ibb.co/dryD2MT
НАЙТИ
Как найти точки С и С2?. По этим точкам построить отрезок С-С2. Главное условие отрезка С-С2, чтобы он был перпендикулярен B1-B2