Здравствуйте, гость ( Вход | Регистрация )
| Alessio |
 30.3.2008, 10:25 30.3.2008, 10:25
Сообщение
#1
|
|
Новичок  Группа: Продвинутые Сообщений: 7 Регистрация: 25.3.2008 Город: Волгоград |
Помогите решить систему уравнений пожалуйста
Эскизы прикрепленных изображений 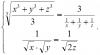
|
Сообщений в этой теме
 Alessio Помогите решить систему уравнений 30.3.2008, 10:25
Alessio Помогите решить систему уравнений 30.3.2008, 10:25
 venja Хитрая система на нестандартные методы. Работа с п... 30.3.2008, 12:57
venja Хитрая система на нестандартные методы. Работа с п... 30.3.2008, 12:57
 Alessio Тыкался-мыкался, никуда =((
Есл это возможно,помог... 30.3.2008, 14:47
Alessio Тыкался-мыкался, никуда =((
Есл это возможно,помог... 30.3.2008, 14:47
 venja
Тыкался-мыкался, никуда =((
Есл это возможно,помо... 30.3.2008, 15:35
venja
Тыкался-мыкался, никуда =((
Есл это возможно,помо... 30.3.2008, 15:35
 Alessio
Жаль. Хотелось бы дать возможность другим получит... 30.3.2008, 16:45
Alessio
Жаль. Хотелось бы дать возможность другим получит... 30.3.2008, 16:45  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | Сейчас: 5.8.2025, 14:25 |
Книжки в помощь: "Сборник заданий по высшей математике" Кузнецов Л.А., "Сборник заданий по высшей математике" Чудесенко В.Ф., "Индивидуальные задания по высшей математике" Рябушко А.П., и другие.
Русская версия Invision Power Board
v2.1.7 © 2025 IPS, Inc.
Зеркало сайта Решебник.Ру - reshebnik.org.ru








